THE GREAT MATHEMATICIANS

MATHEMATICIAN ARYABHATTA

Biography : While there is a tendency to misspell his name as "Aryabhatta" by analogy with other names having the "bhatta" suffix, his name is properly spelled Aryabhata: every astronomical text spells his name thus,^[7] including Brahmagupta's references to him "in more than a hundred places by name".^[8]Furthermore, in most instances "Aryabhatta" would not fit the metre either.^[7

ARYABHATA AND THE DISCOVERY OF PI

Ancient India’s most famous mathematician and astronomer Aryabhata is widely recognized for contributing the concept of zero to the world. As we know zero has formed the basis for the evolution of modern mathematics.
A lesser known fact perhaps is his work on the discovery of the important mathematical constant pi (π). Pi has applications in mathematical calculations and various aspects of science and engineering.
Ancient India in Vedic Times
The Vedic period was a particularly golden period in Indian history, flush with discoveries and inventions in various areas of science, mathematics, arts and culture. Unfortunately, these discoveries (including Aryabhata’s discovery of pi) were buried in the sands of time. And when the western world discovered these concepts, they were hailed as breakthroughs, with no one suspecting that the knowledge was already present in India ages ago.

Born circa 476AD, Aryabhata was present during the Vedic period of India’s history. A highly intelligent individual, he was a Sanskrit scholar with deep interest in astronomy and mathematics. His seminal work ‘Aryabhatiya’ is a compendium of mathematics and astronomy, which has survived till modern times. Studying the ‘Aryabhatiya’ shows beyond doubt that Aryabhata had indeed discovered and worked on concept of pi long before the Western world was even aware of its existence.

Place value system and zero

The place-value system, first seen in the 3rd-century Bakhshali Manuscript, was clearly in place in his work. While he did not use a symbol for zero, the French mathematician Georges Ifrah argues that knowledge of zero was implicit in Aryabhata’s place-value system as a place holder for the powers of ten with null coefficients

However, Aryabhata did not use the Brahmi numerals. Continuing the Sanskritic tradition from Vedic times, he used letters of the alphabet to denote numbers, expressing quantities, such as the table of sines in a mnemonic form.

Trigonometry

In Ganitapada 6, Aryabhata gives the area of a triangle as

tribhujasya phalashariram samadalakoti bhujardhasamvargah

that translates to: “for a triangle, the result of a perpendicular with the half-side is the area.”

Aryabhata discussed the concept of sine in his work by the name of ardha-jya, which literally means “half-chord”. For simplicity, people started calling it jya. When Arabic writers translated his works from Sanskritinto Arabic, they referred it as jiba. However, in Arabic writings, vowels are omitted, and it was abbreviated as jb. Later writers substituted it with jaib, meaning “pocket” or “fold (in a garment)”. (In Arabic, jiba is a meaningless word.) Later in the 12th century, when Gherardo of Cremona translated these writings from Arabic into Latin, he replaced the Arabic jaib with its Latin counterpart, sinus, which means “cove” or “bay”; thence comes the English sine. Alphabetic code has been used by him to define a set of increments. If we use Aryabhata’s table and calculate the value of sin(30) (corresponding to hasjha) which is 1719/3438 = 0.5; the value is correct. His alphabetic code is commonly known as the Aryabhata cipher.

Algebra

In Aryabhatiya Aryabhata provided elegant results for the summation of series of squares and cubes:

and

 (see squared triangular number)

Aryabhata was born in 476 A.D. in Ashmaka, lived in Kusumapura and died in 629 A.D. He is called the first of the great astronomers of the classical age of India . Aryabhata is sometimes called to be the one who gave the world the digit zero.

BRAHMAGUPTA

Against the popular perception, I would say that none including Aryabhat has invented ‘zero’ because the concept of ‘zero’ was always part of our life in different way academically or professionally since the origin of the universe.

Brahagupata’s major contribution to modern science and technology was - how to use zero in mathematical calculations that is used as base to calculate every field. He has formed the set of rules in the mathematics for positive and negative number in addition to forming the rules for using zeros in calculations and that has become the basis of mathematics and rest of the field including economics, finance, physics, chemistry, astronomy and so on…

Brahmagupta was born in 598 CE and died in c. 670. He lived in during king Vyagrahamukha in Bhillamala (modern Bhinmal) a capital of Gurjaradesa Chapa dynasty, one of the largesst kingdoms of Western India in parts of southern Rajasthan and Northern Gujarat.

He studied 5 traditional siddhantas in Brahmapaska in one of top schools for the astronomy during those days.

He also studied his predecessors’ (Aryabhata I, Latadeva, Pradyumna, Varahamihira, Simha, Srisena, Vijayanandin and Vishnuchandra) work to continue their research work. His rules of zero is in continuation of Aryabhata I ‘s work.

Algebra[edit]

Brahmagupta gave the solution of the general linear equation in chapter eighteen of Brahmasphutasiddhanta,

The difference between rupas, when inverted and divided by the difference of the unknowns, is the unknown in the equation. The rupas are [subtracted on the side] below that from which the square and the unknown are to be subtracted.^[14]

which is a solution for the equation bx + c = dx + e equivalent to x = e − c/b − d, where rupas refers to the constants c and e. He further gave two equivalent solutions to the general quadratic equation

18.44. Diminish by the middle [number] the square-root of the rupas multiplied by four times the square and increased by the square of the middle [number]; divide the remainder by twice the square. [The result is] the middle [number].
18.45. Whatever is the square-root of the rupas multiplied by the square [and] increased by the square of half the unknown, diminish that by half the unknown [and] divide [the remainder] by its square. [The result is] the unknown.^[14]

which are, respectively, solutions for the equation ax² + bx = c equivalent to,

${\displaystyle x={\frac {{\sqrt {4ac+b^{2}}}-b}{2a}}}$

and

${\displaystyle x={\frac {{\sqrt {ac+{\tfrac {b^{2}}{4}}}}-{\tfrac {b}{2}}}{a}}.}$

He went on to solve systems of simultaneous indeterminate equations stating that the desired variable must first be isolated, and then the equation must be divided by the desired variable's coefficient. In particular, he recommended using "the pulverizer" to solve equations with multiple unknowns.

18.51. Subtract the colors different from the first color. [The remainder] divided by the first [color's coefficient] is the measure of the first. [Terms] two by two [are] considered [when reduced to] similar divisors, [and so on] repeatedly. If there are many [colors], the pulverizer [is to be used]

 

PYTHAGORAS

Pythagoras was born in approximately 569 B.C. His father was Mnesarchus and his mother was Pythais. Pythagoras spent his early years in Samos. There is little known about his child hood and all physical descriptions of Pythagoras are said to be fictitious except for the vivid birthmark on his thigh. It is believed that he had two brothers and some believe there were three.

Pythagoras was extremely well educated. There were three philosophers that influenced him while he was young. One of the most important of these man was a man named Pherekydes. The philosopher that introduced Pythagoras to mathematical ideas was Thales , who lived in Miletus. It was because of Thales that Pythagoras became interested in math, astronomy and cosmology

.

Pythagoras was interested in all principles of mathematics. He was intrigued by the concept of numbers and basically numbers themselves. Pythagoras had a theory that all relations were able to be reduced in to some form of number. Pythagoras also derived a theory on ratios and scales being produced with the sound of vibrating strings. He made large contributions to music theory.

He studied many different types of numbers ,for example triangles, odd numbers and perfect squares. He believed that each number had its own personality traits and were all different and unique. For example ten is the best number because it contains four consecutive integers (1+2+3+4=10)

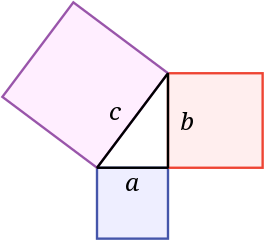
Pythagoras’ greatest contribution to the mathematical society of today is Pythagoras theorem. It is believed that the theory of a²+b²=c² was known to the Babylonians 1000 years before Pythagoras but it was he who was able to prove it.

Pythagoras' greatest contribution to the mathematical society of today isPythagoras theorem. It is believed that the theory of a²+b²=c² was known to the Babylonians 1000 years before Pythagoras but it was he who was able to prove it. 1.The sum of the angle is a triangles equal to two right angles.

Pythagorean theorem

Since the fourth century AD, Pythagoras has commonly been given credit for discovering the Pythagorean theorem, a theorem in geometry that states that in a right-angled triangle the area of the square on the hypotenuse (the side opposite the right angle) is equal to the sum of the areas of the squares of the other two sides—that is, ${\displaystyle a^{2}+b^{2}=c^{2}}$.

While the theorem that now bears his name was known and previously utilised by the Babylonians and Indians, he, or his students, are often said to have constructed the first proof. It must, however, be stressed that the way in which the Babylonians handled Pythagorean numbers implies that they knew that the principle was generally applicable, and knew some kind of proof, which has not yet been found in the (still largely unpublished) cuneiform sources.^[65] Because of the secretive nature of his school and the custom of its students to attribute everything to their teacher, there is no evidence that Pythagoras himself worked on or proved this theorem. For that matter, there is no evidence that he worked on any mathematical or meta-mathematical problems. Some attribute it as a carefully constructed myth by followers of Plato over two centuries after the death of Pythagoras, mainly to bolster the case for Platonic meta-physics, which resonate well with the ideas they attributed to Pythagoras. This attribution has stuck down the centuries up to modern times.^[66] The earliest known mention of Pythagoras's name in connection with the theorem occurred five centuries after his death, in the writings of Cicero

Pythagoras is believed to have died around 500 B.C. He is known for the Pythagorean Theorem, a theorem detailing the relationship between the hypotenuse and legs of a right triangle. Stories about his death include that of his demise at the hands of an angry mob. Other reports indicate that he may have starved himself to death. Others indicate that Pythagoras was killed by the Syracusans as a result of being caught in a conflict between them and the Agrigentum.